本人当前研究方向为影响力最大化（基于机器学习的组合优化算法）。目前在学习陈卫编著的《大数据传播模型与算法》，该系列会定期分享影响力最大化的学习内容（持续更新……），希望大家能够一起交流学习！

前言

1. 什么是影响？
2. 什么是影响力？
3. 什么是影响力最大化？
4. 影响来自哪里？
5. 影响如何传播？
6. 在我们生活中有哪些直观应用？

1. 什么是影响？

我们的各种选择和决定常常受到家人、同事、朋友以及更广泛的大众倾向的影响。举个简单的例子，我在一家餐厅吃饭，我觉得非常好吃并把该观点分享给我的朋友，这就是我对朋友观点的影响。

2. 什么是影响力？

我们受到每一个人，每一个事物影响的程度都是影响力。

3. 什么是影响力最大化？

影响力最大化（IM）是一种经典的组合优化问题，旨在选择少数用户，从而最大限度地扩大在线社交影响力。

4. 影响来自哪里？

企业推广新产品、公益机构推动公益事业、政府扩大政策影响或抵御谣言，都是影响力的来源与应用场景。

5. 影响如何传播？

Christakis 和 Fowler 验证了肥胖症和吸烟行为会在社交网络中传播。在抖音、B站、小红书等平台分享作品，观看者便会受到影响。

6. 在我们生活中有哪些直观应用？

应用于病毒营销、网络监控、谣言屏蔽、社交推荐等领域。

第一章 网络传播模型概述和分类

网络传播模型的种类繁多，侧重点各不同。

1. 基本概念

• 实体：代表网络传播中的对象。
• 有向图 $G=(V,E)$：$V$ 代表结点，$E$ 代表有向边。
• 有向边 $(u,v) \in E$：$u$ 是 $v$ 的入邻居，$v$ 是 $u$ 的出邻居。
• $N^+(v)$：节点 $v$ 的出邻居集合，大小为出度。
• $N^-(v)$：节点 $v$ 的入邻居集合，大小为入度。

2. 网络传播模型及分类

定义 1.1（随机传播模型）： 由图结构、状态空间、概率空间、时间序列及传播函数 $F_v: \Sigma^{N^-(v) \cup {v}} \times \Omega \to \Sigma$ 刻画。

第二章 影响力传播的基本模型

• 影响力拓展度：种子集合 $S_0$ 在时刻 $t$ 活跃节点个数的期望值 $\sigma_t(S_0)$。

1. 独立级联模型 (Independent Cascade Model)

由影响概率 $p(u,v)$ 唯一确定。每个刚激活的点有一次机会激活其邻居，尝试独立。

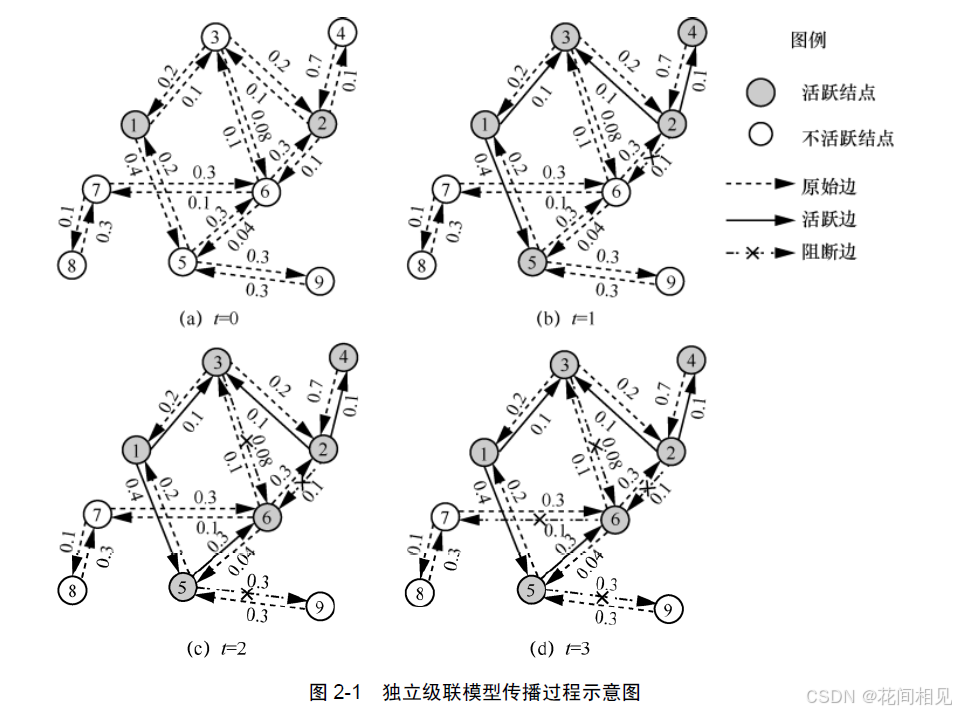
2. 线性阈值模型 (Linear Threshold Model)

由权值 $w(u,v)$ 和随机阈值 $\theta_v$ 确定。激活条件为：$\sum_{u \in N^-(v) \cap S_{t-1}} w(u,v) \geq \theta_v$。

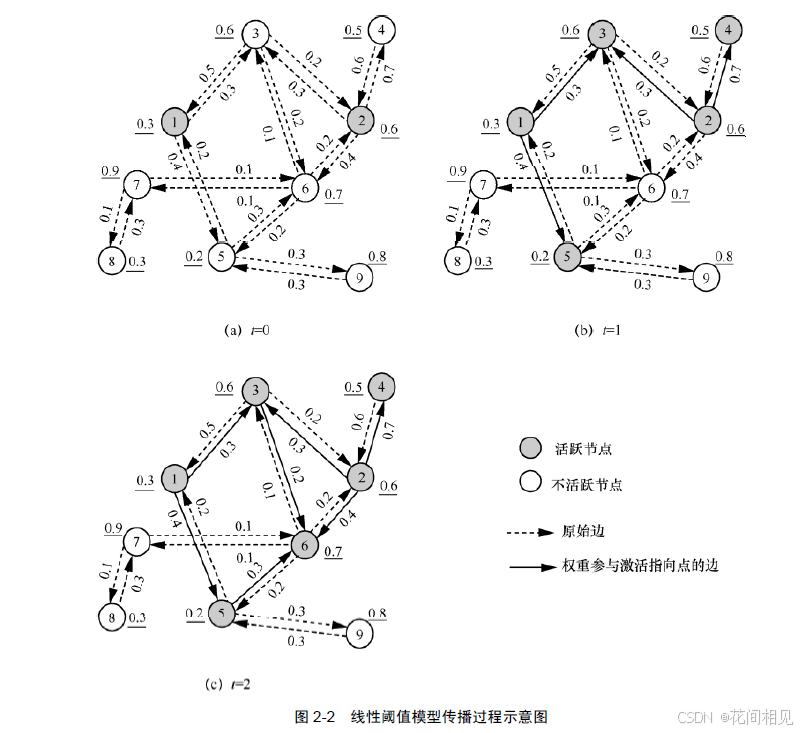
3. 触发模型 (Triggering Model)

每个结点 $v$ 独立采样一个触发集 $T_v$，若触发集中任一结点被激活，则 $v$ 被激活。

4. 通用级联模型和通用阈值模型

| 模型 | 激活阈值 | 节点阈值 | | :—: | :—: | :—: | | 触发模型 | 节点 $v$ 的激活阈值 $[0,1]$ | 阈值随机 | | 通用阈值模型 | 激活阈值由通用函数 $f_v$ 决定 | 阈值随机 | | 线性阈值模型 | 激活阈值由线性函数 $f_v$ 决定 | 阈值随机 | | 固定阈值函数 | 激活阈值由通用函数 $f_v$ 决定 | 阈值固定 |

5. 传播模型的次模性

次模性反映了增量效应递减。详见：次模性理论和应用。

第三章 影响力拓展度计算

1. 蒙特卡洛近似 (Monte Carlo Simulation)

反复模拟传播过程并取平均值。详情参考：蒙特卡洛模拟近似。

2. 特殊图的精确计算

包含基于独立级联模型的出向树、入向树，以及线性阈值模型下的 DAG 计算方法。

第四章 影响力最大化问题和算法

1. 影响力最大化问题定义

在预算 $k$ 下，找到 $S_0^* \in \operatorname{argmax}_{S_0 \subseteq V, |S_0| \leq k} \sigma(S_0)$。

2. 贪心算法

基于单调次模性，贪心算法可保证 $(1 - 1/e)$ 的近似比。

第五章 基于反向影响力采样的算法

1. 反向可达集 (RR-Set)

从随机节点出发反向模拟传播。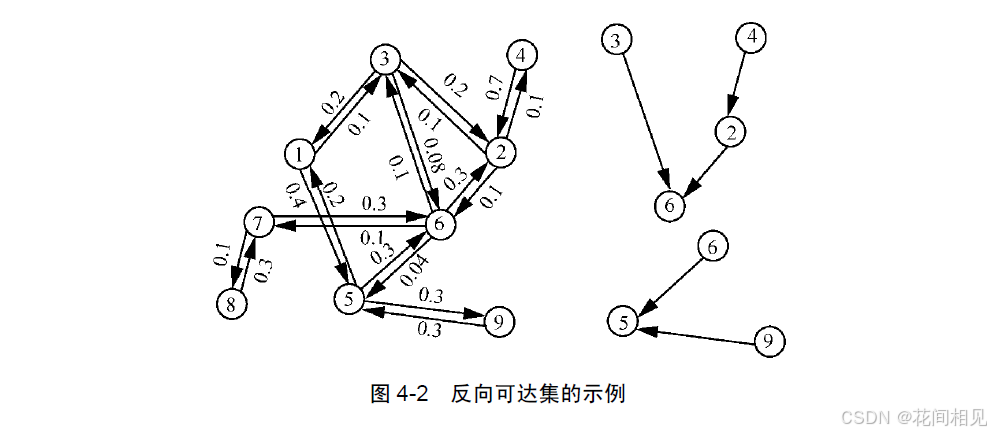

2. IMM 算法步骤

（待更新…）